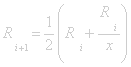Dati due numeri relativi, stabilire, senza effettuare il calcolo, il segno del loro prodotto.

2

Dati due numeri relativi, stabilire, senza effettuare l'operazione, se la loro somma è uguale a zero.

Dati due numeri interi, stabilire, senza effettuare il calcolo, se il loro prodotto è pari o dispari.

Letti due numeri relativi, stabilire, senza effettuare il calcolo, il segno della loro somma (effettuare un controllo sul segno e sul valore assoluto dei numeri dati).

Dati due numeri interi, stabilire, senza effettuare il calcolo, se la loro somma è pari o dispari.

Letti due numeri relativi, stabilire, senza effettuare il calcolo, il segno della differenza (effettuare un controllo sul segno e sul valore assoluto dei numeri dati).

Data la base e l'esponente intero di una potenza, stabilire senza effettuare il calcolo, il segno di tale potenza.

Data la base intera e l'esponente intero di una potenza, stabilire senza effettuare il calcolo, se tale potenza risulta pari o dispari.

Dato un numero relativo, calcolarne, se possibile, la radice quadrata.

Dato un numero relativo, calcolarne, se possibile, la radice cubica del suo reciproco.

Dati due numeri relativi, calcolare, se possibile, la radice quadrata della loro somma.

Dati due numeri relativi, calcolare, se possibile, la radice quadrata del reciproco della loro somma.

Dati due numeri relativi a e b ed il numero relativo n, calcolare la potenza ennesima del rapporto a:b.

Scrivere un programma che, letti i coefficienti a e b dell'equazione: a•x + b = 0 e letto un valore da assegnare alla variabile x, stabilisca se tale valore è soluzione dell'equazione data.

Scrivere un programma che, letta l'equazione:

(k + 1) x = k

ne determini la soluzione dopo aver assegnato, da tastiera, un valore al parametro k.

(Controllare se i valori forniti annullano il coefficiente della x).

16

Scrivere un programma, letta l'equazione:

(a2 - 1) x = a + 1

ne determini la soluzione dopo aver assegnato, da tastiera, un valore al parametro a.

(Controllare se i valori forniti annullano il coefficiente della x o se annullano contemporaneamente coefficiente della x e termine noto).

17

Scrivere un programma che, letta la disequazione:

(a + 1) x < a

ne determini le soluzioni dopo aver assegnato, da tastiera, un valore al parametro a.

(Controllare il segno del coefficiente a + 1 al variare del valore assegnato ad a).

18

Scrivere un programma che, letti i coefficienti dell'equazione di primo grado a due incognite:

a•x + b•y = c

individui, se esistono, le soluzioni dell'equazione nell'insieme:

A = {(x ; y) | x * N * y * N, con x £ 100 e y £ 100}

19

Scrivere un programma che, lette le e-quazioni di primo grado a due incognite componenti un sistema e forniti da tastiera due valori numerici da attribuire alle incognite, verifichi se tale coppia di numeri è soluzione del sistema.

(Controlla prima se la coppia di numeri verifica un'equazione quindi.....).

20

Dato un numero intero positivo N determinare se è perfetto. Un numero perfetto è un intero che è uguale alla somma di tutti i suoi divisori ad eccezione di se stesso. Ad esempio 6 è un numero perfetto poiché 6 = 3 + 2 + 1.

I numeri perfetti trovati sono tutti pari e soddisfano alla formula data da Euclide

2p-1 (2p - 1)

dove p, 2p - 1 sono numeri primi.

Determinare alcuni numeri perfetti.

[6, 28, 496, 8128, ...]

21

Data un'equazione di II grado numerica, determinare se le soluzioni sono reali, e in questo caso valutarne il segno. (Regola di Cartesio).

22

Attraverso la generalizzazione del metodo di Cramer (Sarrus) risolvere un sistema lineare di tre equazioni in tre incognite.

23

Trovare gli zeri razionali di un polinomio. (Ruffini)

24

Determinare l'equazione biquadratica avente per radici quattro valori forniti come dati in ingresso. [Prima della lettura dei dati accertarsi se i valori forniti sono reali o immaginari].

25

Dati i coefficienti ed il grado dell'equazione trinomia:

ax2 + bx + c = 0

calcolare, se esistono, le soluzioni reali.

(Controllare il discriminante dell'equazione di secondo grado associata e verificare se l'equazione binomia ottenuta ammette soluzioni reali).

26

Determinare due numeri la cui somma e il cui prodotto siano uguali rispettivamente ad S e P.

27

Dati i coefficienti a, b, c del trinomio di secondo grado ax2 + bx + c, determini, se esistono, i binomi a coefficienti reali in cui il trinomio può essere scomposto.

28

Dati due valori x1 e x2, determini l'equazione di secondo grado avente come soluzioni x1 e x2.

29

Dati i coefficienti a, b, c di un'equazione di secondo grado, il valore da assegnare alla variabile x, stabilire se tale valore è soluzione dell'equazione: ax2 + bx + c = 0.

30

Dati i coefficienti a, b, c dell'equazione di secondo grado: ax2 + bx + c = 0 senza risolverla, indicare:

- la natura delle radici;

- la somma delle radici;

- il prodotto delle radici;

- in caso di realtà, i segni delle radici.

31

Dato un numero intero positivo N, stabilire se è primo ed in caso negativo, scomporlo in fattori.

32

Determinare la successione dei numeri triangolari minori di un limite dato. I numeri triangolari sono 1, 3, 6, 10, ..... determinabili mediante la relazione di ricorrenza: tn = tn + n per n = 2, 3, 4, ... essendo t1 = 1 e prendono tale nome perché‚ permettono la realizzazione di triangoli.

33

Determinare il M.C.D. e il m.c.m. di due numeri interi positivi.

34

Convertire un numero intero in base dieci in una base arbitraria compresa fra 2 e dieci.

35

Dato un numero binario determinare la corrispondente rappresentazione decimale.

36

Dato un polinomio nella forma ax2 + bx + c stabilire se è divisibile per un polinomio (x - d).

37

Stabilire, utilizzando i criteri di divisibilità, se un numero è divisibile per 3.

38

Stabilire, utilizzando i criteri di divisibilità, se un numero è divisibile per 5.

39

Stabilire, utilizzando i criteri di divisibilità, se un numero è divisibile per 11.

40

Determinare la moltiplicazione tra due frazioni.

41

Determinare la divisione tra due frazioni.

42

Determinare il mcm di due numeri supponendo di averli già scomposti in fattori primi.
[Applicate la regola: il mcm è dato dal prodotto dei fattori primi comuni e non comuni presi una sola volta, con il massimo esponente].

43

Determinare il MCD di due numeri supponendo di averli già scomposti in fattori primi.

44

Dati i coefficienti ed il grado dell'equazione trinomia: ax2n + bxn + c = 0 calcolare e stampare, se esistono, le soluzioni reali.
Controllare il discriminante dell'equazione di secondo grado associata e verificare se l'equazione binomia ottenuta ammette soluzioni reali).

45

Dati i radicali aritmetici:

con n,m Î N ed a,b Î R+, costruire un diagramma a blocchi e stendere il relativo programma che, letti i valori di m, n, a, b, calcoli la somma dei due radicali.

(Controllare se a=b e n=m).

46

Dati i radicali aritmetici:



con n,m Î N ed a,b Î R+, costruire un diagramma a blocchi e stendere il relativo programma che, letti i valori di m, n, a, b, calcoli il prodotto ed il quoziente dei due radicali.

47

Un polinomio omogeneo e completo in x di grado n è una scrittura del tipo seguente:

P(x) = an • xn + an-1 • xn-1 + .... + a1 • x + a0

dove con i pedici decrescenti da n a 0 sono contrassegnati i coefficienti dei termini di grado da n a 0.

Il polinomio ammette come divisore il binomio

(x + z)

con z numero reale, se si annulla per x=z, cioè se P(z), resto della divisione tra P(x) e (x + z), vale 0.

Pertanto per verificare la divisibilità di P(x) per (x + z) è sufficiente calcolare P(z) e confrontare con 0 il suo valore.

48

Calcolo di coefficienti binomiali

49

La configurazione seguente:


1

1 1

1 2 1

1 3 3 1

1 4 6 .....

detta triangolo di Tartaglia o anche triangolo di Pascal, è studiata perché fornisce i coefficienti del binomio di Newton


(a + b)n, per n = 3:

(a + b)3 = a3 + 3a2b + 3ab2 + b3

Un modo per compilare il triangolo fa uso dei coefficienti binomiali, e precisamente dà gli elementi come coefficienti binomiali in funzione della riga, cioè dell'esponente assegnato al binomio:


riga 0:

riga 1:

riga 2:

riga 3:

......................................................

riga k: .....

......................................................
 

50

Calcolare le soluzioni di un sistema di sue disequazioni di primo grado ad una incognita.

51

Calcolare le soluzioni di un'equazione di primo grado del tipo (a + b) x = a + 2 • b, con 'a' e 'b' numeri reali qualsiasi.

52

Scomporre in fattori un trinomio di secondo grado, del tipo ax2 + bx + c, supponendo il discriminante positivo. A tale scopo sarà necessario risolvere prima l'equazione ottenuta uguagliando a zero il polinomio e, indicate con x1 e x2 le soluzioni, applicare la formula: ax2 + bx + c = a (x-x1) (x-x2).

53

Dividere un polinomio di grado inferiore o uguale a 5 per un polinomio di primo gra-do nella stessa incognita x, determinando quoziente e resto mediante la regola di Ruffini.

54

Calcolare due numeri x1 e x2 dei quali siano noti la somma (x1+x2=s) e il prodotto (x1•x2=p).

55

A partire dalla tabulazione di una funzione in un intervallo assegnato, calcolare i sottointervalli in cui essa risulta crescente e quelli in cui è decrescente. Si effettui tale analisi mediante lo studio dei segni delle differenze, tra un valore e il precedente, della funzione desiderata.

56

Dato un numero intero positivo n, si chiama funzione di Eulero, F(n), il numero di interi, compresi fra 1 e n stesso, che sono primi con il numero considerato (due numeri si dicono primi tra loro se il loro massimo comun divisore è uno). Avremo così che F(3)=2, perché 1 e 2 so-no primi con 3; F(4)=2, in quanto 1 e 3 sono primi con 4, e così via. Calcolare la funzione F(n) per n intero positivo immesso da tastiera. Si può utilizzare l'algoritmo di Euclide all'interno di un'iterazione che calcoli il massimo comun divisore tra i numeri minori di n e n stesso e che conti i numeri che sono primi con il numero assegnato.

57

Si chiama progressione aritmetica una successione di numeri tali che la differenza tra un qualunque numero e il precedente sia costante (ragione della progressione). Calcolare, a partire dal valore iniziale e dalla ragione, i termini della progressione inferiori ad un valore numerico prefissato.

58

Si chiama progressione geometrica una successione di numeri tali che il quoziente tra un qualunque numero e il precedente sia costante (ragione della progressione). Calcolare, a partire dal valore iniziale e dalla ragione, i termini della progressione inferiori a un valore numerico fissato.

59

Costruire un algoritmo che calcoli il valore dell'espressione:

Sn = 1 + 1/2 + 1/3 + 1/4 + ....... + 1/n

dove n è un numero naturale letto in ingresso.

60

Costruire un algoritmo che calcoli il valore dell'espressione:

Sn = 1 + 1/2 + 3 + 1/4 + 5 + 1/6 + ....... + 1/n

dove l'ultimo denominatore n è un numero pari.

61

Costruire un algoritmo capace di individuare, tra i numeri naturali di una lista, quelli divisibili per un determinato numero naturale b ¹ 0.

62

La successione di Fibonacci è così definita:

F1 = 1, F2 = 1, Fi+2 = Fi + Fi+1

Ad esempio i primi 6 elementi della successione sono : 1, 1, 2, 3, 5, 8.

Si descrivano i diagrammi a blocchi dei seguenti algoritmi:

a] per il calcolo dell'n-esimo elemento della successione;

b] per il calcolo dell'indice k del primo elemento Fk maggiore di un valore dato d;

c] per il calcolo dei primi n numeri del-la successione;

d] per il calcolo della differenza tra l'n esimo e l'm esimo elemento della successione.

63

Gottfried Wilehlm Leibniz (1646-1716) studiò il triangolo armonico:
 

Scrivere un programma che stampi il triangolo armonico fino alla riga N (N fornito in input).

64

Verificare che si ha:

65

Determinare alcuni numeri naturali automorfi, ossia che si presentano all'estremità del rispettivo quadrato: ossia, ab è automorfo se il suo quadrato è cab.

[0, 1, 5, 6, 25, ...]

66

Determinare alcuni numeri naturali di due o più cifre che godono della seguente proprietà: se denotiamo con ab un numero di due cifre, elevando ab al quadrato, invertendo le cifre del quadrato ed estra-endo la radice quadrata di quest'ultimo numero si ottiene il numero ba.

[12; 13; 112; 113; ...]

67

Determinare le coppie di numeri naturali rispettivamente di due, tre, quattro, ,,,,, ci-fre, i cui quadrati sono formati con le stesse cifre.

[12 • 42 = 21 • 24; 12 • 63 = 21 • 36; ...]

68

Determinare le coppie di numeri naturali consecutivi di due, tre, quattro, .... cifre, i cui quadrati sono formati con le stesse cifre.

[132 = 169, 142 = 196; 157, 158; 913, 914; ...]

69

Si dicono numeri amici o amicabili quelle coppie di numeri naturali tali che la somma dei divisori dell'uno, escluso il numero stesso, sia uguale all'altro e viceversa.

Determinare alcune coppie di numeri amici.

[220, 284; 1184, 1210; ....]

70

Ogni numero primo p che si può mettere nella forma

p = 4 x + 1, x Î N

può essere scomposto come somma di due quadrati.

Ad esempio: 5 = 4 • 1 + 1 = 12 + 22.

Trovare alcuni di tali numeri primi.

[5, 13, 17, ....]

71

Trovare il Minimo Comune Multiplo tra due numeri n ed m servendosi della seguente idea: sommare ripetutamente il più piccolo dei due all'altro fino a quando non diventano uguali. Assicurarsi che il programma funzioni anche per n=m.

72

Due numeri n ed n+2 si dicono gemelli se n ed n+2 sono primi. Scrivere un programma che, dato n, stabilisca se n ed n+2 sono gemelli.

73

Scrivere un programma che scrive una sola volta tutti i fattori primi di un intero n>1.

74

Algoritmo di Newton-Raphson. Per trovare la radice quadrata di un numero x³0 si può fare uso della seguente successione:

R0 = x

Scrivere un programma che legga un numero x*0 e dia in uscita la radice di x ottenuta arrestando la successione quando la differenza con l'elemento precedente risulta minore di 0.001.

75

Esiste un metodo antichissimo per trovare tutti i numeri primi compresi fra 2 e n noto come Crivello di Eratostene. Esso consiste nello scrivere di seguito tutti in numeri fra 2 ed n e nel cancellare successivamente tutti i multipli di 2 (eccetto 2), tutti i multipli di 3 (eccetto 3), tutti i multipli di 5 (il 4 e i suoi multipli sono già stati cancellati) e così via fino a superare n (perché?). I numeri sopravvissuti a questo «settacciamento» saranno tutti e soli i numeri primi compresi fra 2 e n. Programmare il metodo.